The Monty Hall Problem Easy Explanation

“Logic is in the eye of the logician.” — Gloria Steinem

Oh boy, do we ever like proving ourselves to be right. After all, it’s what fuels social media and our ever-rising disdain for each other. But it’s not just politics and cultural issues that drive us to rage against the human machine, even simple non-consequential hypotheticals can do it, too.

Case in point:

• The advice columnist Ann Landers once received over 15,000 letters after jestingly stating which side toilet paper should hang on (it’s over, by the way).
• Nerds all over the world continually debate the best video game of all time (Mariokart, of course).
• Foodies have been locked in a battle for millennia to determine what is the single best dish (peanut butter tuna sandwiches, duh).

The list of controversies is unending, but this simple logic test based on an old game show has to be one of the weirdest — and hotly debated — ones to ever exist.

It’s usually referred to as the Monty Hall problem, and it takes a minute to wrap your head around it.

The history of the Monty Hall problem

Back in the 70s, the prolific statistician Steve Selvin sent a letter to the American Statistician magazine simply titled A Problem in Probability. Inside, he outlined an interesting hypothetical situation alongside a proposed solution.

After receiving ample amounts of criticism from his fellow statisticians, he sent a follow-up solution he called The Monty Hall problem, named after a popular game show host of the era, with an alternative explanation based on Bayes’ Theorem.

Then 15 years later in 1990, Marilyn vos Savant, the former Guinness book of world records holder for the highest IQ ever recorded, shared the problem in her popular question and answer column at Parade Magazine.

The result?

Almost 10,000 mostly-angry letters were sent to the magazine, including over 1,000 from PhD holders, with the vast majority of them stating she was clearly wrong.

What could inspire so many people — many of whom were the most educated in America — to take precious time out of their day to notify a stranger they were wrong about something so inconsequential?

Well, arrogance for one. And misunderstanding for the other.

But to find out the full answer, let’s jump into what the actual logic puzzle is and why it is so damn perplexing to people.

What is the Monty Hall problem?

Imagine you’re a guest on a gameshow and in front of you are three doors.

Behind these doors are three potential prizes, two nasty little goats and one shiny sports car. The goats and the flashy crypto-bro’s car can be behind any of the doors at random. But, the game show host also knows which prize is behind which door.

The game then goes like this:

1. You are allowed to choose one door you want to open (but it isn’t opened until later).
2. The host then opens one of the two remaining closed doors.
3. After the door is opened and you see what’s behind it, you have the choice to change your choice of door or leave it as is.
4. The host then opens the final door you chose, where you’ll see if you win either a goat or a car.

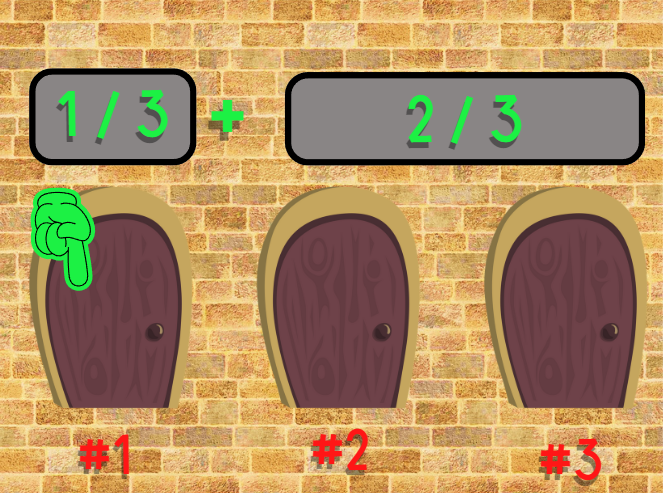
“So the main question is, do you choose to switch your door after the host opens one?”

In the above image, you chose door #1, then the host opened door #3, revealing a goat. Now you have the choice of keeping your selection of door #1 or switching to door #2.

What do you do?

At the beginning of the game, most people would correctly assume your chance of winning the car is 1/3.

But then it gets slightly trickier because of the following conditions:

1. The host must always open a door that wasn’t picked by you.
2. The host will always open a door that has a goat behind it and at random (because they don’t want you winning a car automatically).
3. The host always offers you a chance to switch between your original door choice or the remaining closed door (remember, he’s already opened up one goat door by this point).

Sounds easy enough right? Choose one of three doors and hope you win the car and not one of the two goats. Two goats, one car. Three doors, one chance to open.

So, knowing all of the above, after the game host opens one of the three doors, do you change which door you want to open at the end?

Note: If the above explanation is too wordy for you, this is how the original question was posed:

“Suppose you’re on a game show, and you’re given the choice of three doors: Behind one door is a car; behind the others, goats. You pick a door, say №1, and the host, who knows what’s behind the doors, opens another door, say №3, which has a goat. He then says to you, ‘Do you want to pick door №2?’ Is it to your advantage to switch your choice?” — From Parade magazine’s Ask Marilyn column

The Monty Hall problem controversy

This is where things get messy. The true answer to the problem is, logically, yes!

You absolutely should change your door choice! Because the odds are higher you’ll win a car if you switch the door instead of keeping your initial selection.

Why?

• If you keep your initial door choice, the chance of a race car being behind the door is only 1/3.
• If you switch your choice, you have a 2/3 chance of winning the car.

Now, if you’re like 87% of people in a study on the problem or named J.J. Pryor, you chose incorrectly. And if you’re like most of the 10,000 letter writers to Marilyn vos Savant, you’re probably a bit angry right now.

People assume the real answer is that it doesn’t matter. That if we have two remaining doors, with only one goat and one car left, the odds have to be 50%.

Two choices, two outcomes, the randomness implies it‘s a simple coin toss, right?

And yet, it can be and has been proven that if you switch your choice from the first door to the remaining unopened door, your odds of winning go up!

How can this be?

This is where it gets even messier.

When you start the game, you have three choices of doors with an equal chance to win the car, each with a 1/3 chance to guess right.

• Door #1 (Closed): 1/3 chance of having a car
• Door #2 (Closed): 1/3 chance of having a car
• Door #3 (Closed): 1/3 chance of having a car

But then the gameshow host changes the environment, he adds information. The host must open a door that doesn’t have a car in every scenario (he doesn’t want to give the race car away).

That leaves you with this set of doors.

• Door #1 (Closed): 1/3 chance of having a car
• Door #2 (Closed): ? chance of having a car
• Door #3 (Opened): 0 chance of having a car because it has an angry goat

This is where our natural logic starts to screw up. We see only two remaining doors, one with a car and one with a goat. Of course, we naturally think we have a 50% of winning the car, regardless of whether we switch our choice or not!

But here’s the mathematical way to think about it, or at least in my own words. The difference comes with when we assess the odds.

At the beginning, the chances really are 1/3, 1/3, 1/3.

So when we chose door #1, its odds were indeed 1/3. That doesn’t change.

The final odds of winning were the odds of Door #1 + Door #2 + Door #3, or 1/3 + 1/3 + 1/3.

But when the door was opened, a door that had to be a goat and not a car, the odds only changed because the game show host knowingly chose a door. As in, his choice wasn’t random. The fact that he couldn’t and didn’t select your choice nor a door with a car behind it changes the outcome and the odds.

Again, the original selection was this:

• Door #1 (Closed): 1/3 chance of having a car
• Door #2 (Closed): 1/3 chance of having a car
• Door #3 (Closed): 1/3 chance of having a car

But after the game show host’s actions, they changed to this:

That’s how our brains typically think of the logic afterward. That there’s only door #1 with a 1/3 chance and door #2 with a 1/3 chance left, which means 50–50 odds. As in, no need to switch our choice, because it’s a coin toss, right?

But in reality, the math works more like this (in a simplified manner, anyway):

If we think of doors #2 and #3 as combined odds, we can all agree it’s 2/3, right?

• 1/3 + 1/3 + 1/3
• 1/3 + 2/3

So, thinking in this manner, when the game show host opens a door that he knows has to contain a goat, we end up with these odds:

• Door #1 (Closed): 1/3 chance of having a car
• Door #2 (Closed) + Door #3 (Open): 2/3 chance of having a car

If you switch your door from #1 to #2, your odds increase to 2/3!

Since the gameshow host won’t open a door with the racecar behind it, it changes the final odds when you get to choose if you want to change the choice.

The odds treat door #2 and #3 as being combined — that is, they both collectively have 2/3 chance of having the race car, and since you can only choose one now, that last choice has a 2/3 chance!

Crazy, right?

Is there another way to view the Monty Hall problem?

It’s often hard for us to wrap our heads around the problem, so it helps to think of it in a few different ways.

I personally like how Cecil Adams once put it.

“Monty is saying in effect: you can keep your one door or you can have the other two doors.”

Another way to view the logic question is if instead of only three doors, there were one hundred — 99 goats and 1 sports car.

You’d choose your door, let’s say door #1. The game host would then open 98 doors, leaving one door closed, let’s say #54.

Now what do you think the chances are that out of 100 doors, you chose the only one with a race car behind it? And now you see only 1 other remaining closed door, #54, and you KNOW the host can’t open a race car door.

The odds are simply 99% you’d win if you switch.

Makes the problem a bit more understandable, n’est pas?

Now, after reading my weird explanations and terrible drawings and you still find yourself not believing me, there are fortunately a lot of other explanations out there.

• For a deep dive into the math and probabilities, check out this page or this one
• For a pictorial explanation, check out this site
• Or you can check out a fun little animated explanation from Numberphile

And that, ladies and gentlemen and angry cartoon goats, is the Monty Hall problem. I can’t wait to see all the agreeableness in the comments!

J.J. Pryor

Head over here for more of my written shenanigans.